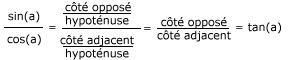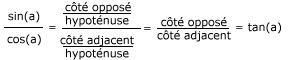1. Sinus-Cosinus-Tangente
Hypothèse d'utilisation
Comme pour le théorème de Pythagore, il faut un triangle rectangle
Soit ABC un triangle rectangle en C.
Définition pour l'angle a :
[AC] s'appelle le côté adjacent et [BC] le côté opposé.
Ø sin (a) = côté opposé / hypoténuse = BC / AB
Ø cos (a)= côté adjacent / hypoténuse = AC / AB
Ø tan (a) = côté opposé / côté adjacent = BC / AC
Définition pour l'angle b : (c'est le contraire)
[AC] s'appelle le côté opposé et [BC] le côté adjacent.
Ø sin (b) = côté opposé / hypoténuse = AC / AB
Ø cos (b)= côté adjacent / hypoténuse = BC / AB
Ø tan (b) = côté opposé / côté adjacent = AC / BC
Premières propriétés :
Ø L'hypoténuse est le plus grand des côtés, donc les valeurs du
sinus et du
cosinus sont comprises
entre 0 et 1.
Ø 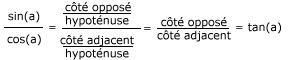
Ceci est vrai pour n'importe quel angle, donc en général :
2. Calcul de longueur
Soit EFG un triangle rectangle en G, tel que GE = 7 cm,
l'angle ê mesure 30°.
a. Calculer EF.
b. Calculer l'angle f.
c. Calculer FG.
a. Utiliser le cosinus
Le triangle EFG est rectangle en G, donc on peut utiliser cosinus.
cos(e) = côté adjacent / hypoténuse = EG / EF
donc cos(30) = 7 / EF
donc EF = 7 / cos(30) = 8.1 cm à 0,1 près.
Remarque :
ØVotre calculatrice doit être en degré et "D" ou "DEG" doit être écrit en petit sur votre écran. Sinon pour les Casio, il faut taper "Mode 4" ou "Mode Mode 1". Pour les autres il faut regarder la notice.
ØSur les calculatrices récentes (Casio collège New, TI 30 ; TI 40) on tape le calcul comme il est écrit. Pour les "vieilles" calculatrices, on ne tape pas "cos 30", mais "30 cos".
b. Calculons l'angle f
On sait que la somme des angles d'un triangles est égale à 180 °
Donc g + e + f = 180.
Donc f = 180 - e - g = 180 - 30 - 90 = 60 °.
c. Utilisation du sinus
Le triangle EFG est rectangle en G, donc on peut utiliser sinus.
sin(e) = côté opposé / hypoténuse = FG / EF
donc sin(30) = FG / 8.1
donc FG = 8.1 x sin(30) = 4 cm à 0,1 près.
3. Calcul des angles
IJK est un triangle rectangle en K.
On sait que : JK = 3 cm et KI = 5 cm.
On veut calculer les angles j et i.
a. L'angle i
JK est le côté opposé à i.
IK est le côté adjacent à i.
On sait que tan(i) =JK / IK = 3 / 5 = 0,6
On va utiliser la fonction inverse de tan sur la calculatrice, pour cela, il faut taper :
Ø Sur les casio Collège New : Seconde tan 0,6 Exe.
Ø Sur les "vieilles" casio : 0,6 Shift tan.
(Sur les autres, il faut lire la notice...)
On trouve dans tous les cas i = 30,96 ° à 0,01 près.
Remarque :
Ø Il faut que vos calculatrice soit en degré.( pas en grad ni en radian)
Ø C'est le même principe que la fonction X² et son inverse : racine carrée.
Ø Les fonctions inverses marchent aussi avec cos et sin, on les utilise quand on connaît l'hypoténuse et un autre coté.
b. L'angle j
JK est le côté adjacent à j.
IK est le côté à opposé j.
On sait que tan(j) =IK / JK = 5 / 3 = 1,6666 (il faut 4 chiffres après la virgule si on veut être précis)
On utilise la fonction inverse de tangente sur la calculatrice, on tape :
Ø Sur les casio Collège New : Seconde tan 1,6666 Exe.
Ø Sur les "vieilles" casio : 1,6666 Shift tan.
On trouve 59,04 ° à 0,01 près.
c. Vérification
La somme des angles d'un triangle est égale à 180°,
donc i + j + k doit être égale à 180 °
30,96 + 59,04 + 90 = 180° : Notre calcul est juste, OUF !!!
Remarque :
Il se peut que on trouve 179,9 ou 180,1 si on a arrondi, mais ce n'est pas grave.