1. Définition-Propriétés
a. Système d'equation à n équations, n inconnues
Un système d'equation à n équation et n inconnues est un ensemble de n égalités dans lesquelles n nombres sont inconnus.
Remarque :
ØEn 4°, vous avez vu les équations avec 1 inconnue. C'est un système à 1 equation, 1 inconnue.
ØEn 3°, on se contentera de voir les systèmes à 2 equations, 2 inconnues et parfois à 3 équations, 3 inconnues en exercice.
ØPour plus de facilité, on dira système 2-2 ou 3-3.
b. Solution d'un système n-n
On appelle solution d'un sytème n-n, un ensemble de n nombres qui vérifie toutes les egalités du système.
Un système n-n a soit :
ØUne solution unique, c'est à dire un seul ensemble de n nombres qui vérifie les n égalité.
ØAucune solution.
ØUne infinité de solution, c'est à dire une infinité d'ensembles de n nombres qui vérifient les n égalités.
c. Exemple
On considère le système 2-2 suivant :
On cherche tous les nombres x et y qui vérifient simultanément l'égalité (1) et l'égalité (2).
La solution est x = 0,5 et y = -0,5.
On note cela S = {(0,5 ; -0,5)} (x est toujours en 1° et y toujours en 2°)
Vérifions que x = 0,5 et y = -0,5 est bien solution : Remplacons x par 0,5 et y par -0,5
ØDans (1) : 0,5 - (-0,5) = 0,5 + 0,5 = 1 c'est bon !!!
ØDans (2) : 0,5 + (-0,5) = 0,5 - 0,5 = 0 c'est encore bon !!!
On considère le système 2-2 suivant :
On cherche tous les nombres x et y qui vérifie simultanément l'égalité (1) et l'égalité (2).
Il n'existe pas de solution car 2x + 2y ne peut pas être à la fois égale à 0 (égalité 2) et à 1 (égalité 1)
On note cela S =
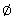 (Ce signe se lit "ensemble vide")
Remarque :
Ø
(Ce signe se lit "ensemble vide")
Remarque :
Ø Dans les exercices de 3° du brevet, il y a 1 solution unique.
Ø On parle de solution unique alors qu'il y a deux nombres x et y car ces deux nombres sont liés.
2. Recherche des solutions par substitution :
On utilise cette méthode quand au moins un des coefficients de x ou y d'une des égalités est 1.
Exemple :
Dans l'égalité (2), le coefficient de x est 1.
On peut donc écrire d'après (2) que x = 2 - 2y
On remplace (ou on substitue) x par 2 - 2y dans (1) : 2(2 - 2y) + 3y = 1
On a 4 - 4y + 3y = 1 (en développant)
donc 4 - y = 1 (c'est une équation que vous connaîssez depuis la 4°)
donc - y = 1 - 4 = - 3
donc y = 3
On sait que x = 2 - 2y = 2 - 2x3 = 2 - 6 = -4
Donc x = -4 et y = 3
On note S = {(-4 ; 3)}
Remarque : Cette méthode s'appelle substitution car on substitue une des variables par sa valeur dans une égalité.
3. Recherche des solutions par combinaison
On utilise cette méthode quand aucun des coefficients de x ou y n'est égal 1.
Cette méthode à l'air compliquée, mais une fois qu'on l'a comprise, elle est très performante.
Exemple :
1° étape : On va multiplier chaque égalité par un nombre pour que les coefficient de x soient égaux.
On multiplie (1) par 3 et (2) par 2 (C'est le même principe que pour réduire deux fractions au même dénominateur)
On obtient :
2° étape : On va soustraire membre à membre (3) - (4) pour éliminer x.
On obtient :
-9y - (-10y) = 3 - 0
donc -9y + 10y = 3
donc y = 3
3° étape : On remplace y par sa valeur dans (1) ou (2) (au choix selon les coefficients).
On remplace dans (2) :
3x - 5x3 = 0 donc 3x = 15 donc x = 15/3 = 5
4° étape : On vérifie les résultats dans l'autre égalité, ici (1).
2x5 - 3x3 = 10 - 9 = 1, C'est bon !!!
5° étape : On écrit la réponse :
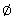 (Ce signe se lit "ensemble vide")
(Ce signe se lit "ensemble vide")