1. Cônes

          a.Définition:

         Un cône est un volume dont la base est un disque. Son sommet est sur la droite qui passe par le centre du disque de base perpendiculairement à cette base. Le cône est engendré par la rotation d'un segment reliant le sommet à un point du cercle de la base.

          b.Exemple:

         Le cône suivant à pour sommet S . Le centre de la base est O. La génératrice est [SA]


          c.Volume:

         Le volume du cône est donné par la formule générale :
         V = (1/3) x (Aire de la base) x (hauteur)
         Ce qui donne V = (1/3) x pi x R² x h.
          et si on applique cette formule à l'exemple b : V = (1/3) x pi x OA² x SO

          d.Aire lattérale:

          L'aire lattérale d'un cône est donné par la formule: (g est la longueur de la génératrice)
          A = pi x R x g
          Si on applique cela à l'exemple b , on a : A = pi x OA x SA


2. Pyramides

         a.Définition:

          Une pyramide à pour base un polygone. Ses faces lattérales sont des triangles qui ont un point commun: Le sommet.

         b.Exemple:

          La pyramide suivante à pour sommet S et pour base le triangle ABC.


         c.Volume:

         Le volume de la pyramide est donné par la formule générale :
         V = (1/3) x (Aire de la base) x (hauteur)

         d.Pyramide régulière:

         On dit qu'une pyramide est régulière si sa base est un polygone régulier et que sa hauteur passe par le centre du cercle circonscrit à sa base.Voici par exemple une pyramide de base le carré ABCD et de sommet S:


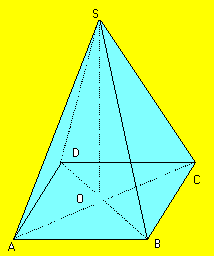
         Son volume est V = 1/3 x AB²x SO

3. Un lien pour ''voir'' la 3D: